sma11new

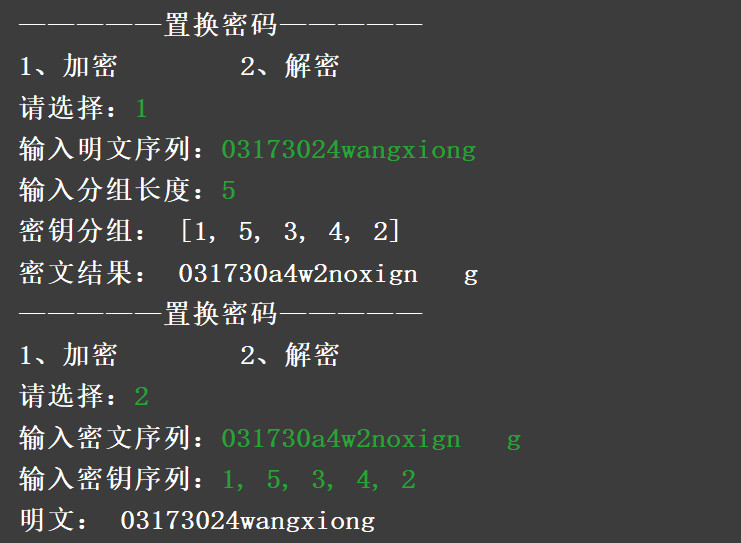
简述置换密码是一种不改变明文字符、只改变字符顺序的加密算法。 加解密： 给出明文字符串，如 abcde，则此时的排序记为 [1，2，3，4，5]给定一个随机序列作为密钥，如 [2，1，4，5，3] 加密 将原始字符串的字符位置，按照密钥的排序位置改变，重新组合。 初始序列：[1，2，3，4，5]置换序列：[2，1，4，5，3] 上述加密结果：[b，a，d，e，c] 解密 将密文序列进行一次密钥的逆置换，即得明文。 初始序列：[1，2，3，4，5]置换序列：[2，1，4，5，3]逆置序列：[2，1，5，3，4] 上述解密结果：[1，2，3，4，5] 即 [a，b，c，d，e] 代码实现12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273#!/usr/bin/python3.7# -*- coding: utf-8 -*-# @Time : 2019/12/ ...

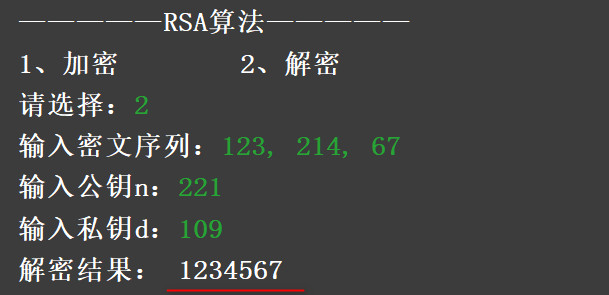
简述RSA加密算法是一种非对称加密算法。在公开密钥加密和电子商业中RSA被广泛使用。 整个加密过程要用到p、q、n、L、E、D六个数据： p、q：选取两个足够大的素数 p、qn：令 n = p * qFn：Fn 是 n 的欧拉函数，（此处为（p-1）乘以（q-1））e：选取一个e使得 1 < e < Fn，且 gcd(e，Fn) = 1d：d 为 1 = e mod Fn 的乘法逆 此时，（e，n）为公钥（d，n）为私钥 加密过程：c = ( m ^ e ) % n 解密过程：m = ( c ^ d ) % n 代码实现123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104 ...

简述仿射密码为单表加密的一种，字母系统中所有字母都藉一简单数学方程加密，对应至数值，或转回字母。 加密：E(x) = (ax + b) (mod m)，其中 a与b互质，m是编码系统中字母的个数（通常都是26）。 解密：D(x) = a^{-1} (x - b) (mod m)，其中 a^{-1} 是 a 在Z_{m}群（此处为26）的乘法逆元。 代码实现12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697# 创建字母表def creatLetterList(): letterList = [] for i in range(ord("a"), ord("z") + 1): letterL ...

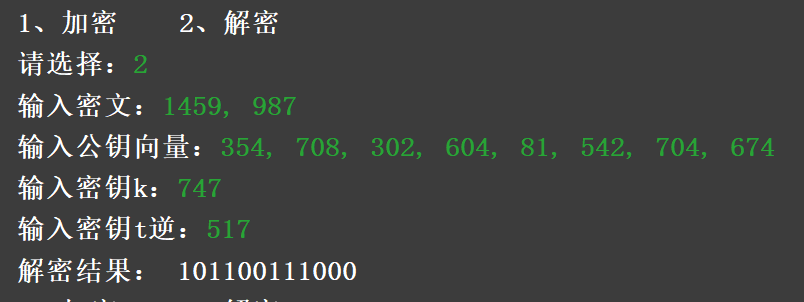
简述 公钥密码 公钥密码又称非对称密码，所谓非对称密码即加解密使用的不是同一个密钥。 在公钥密码体系中，使用每个人拥有两种密钥，公钥和私钥，公钥是公开的，用来加密，私钥是私自保存的，用于解密。如：只有用自己的私钥才能解开自己公钥加密的信息，而且通过公钥钥是不能推出私钥的。 公钥密码将辅助信息（陷门信息）作为私钥，这类密码的安全强度取决于它所依据的问题的计算复杂度。 常见的公钥密码有RSA公钥密码、ElGamal公钥密码、椭圆曲线密码。 背包问题 背包问题：假设有一堆物品，体积各不相同，问能否从这堆物品中找出几个正好装满一个给定容量的背包？（假定物品之间不留空隙）记物品的体积分别为v1，V2，…，n，背包的容量为C，则背包问题可表示为：b1v1＋b2v2＋…＋bnvn＝C，其中，bi（i＝1，2，…，n）等于1或者0。 bi = 1表示第i个物品在背包中，bi＝0表示第i个物品不在背包中，称物品体积的序列（v1，V2，…，vn）为背包向量。 目前没有一个高效的算法来解决这个问题，只是进行穷举式搜索，但当数据足够多时，达到2的1024或2048位时，穷举式搜索将不再现实，问 ...

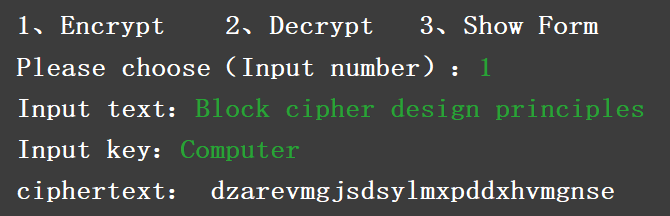
简述维吉尼亚密码是在代换密码（即单表代换）基础上，衍生出来的多表代换密码。 与单表代换相同，维吉尼亚密码也采用明文字母与密钥字母（即26字母表）间建立一一对应关系。 但是不同的是，单表代换密码中一旦密钥字母确定，相同的明文就只能产生唯一的密文； 而维吉尼亚密码则是在单表的基础上，加入了密钥字，使用密钥字对明文进行分组加密，因此即使密钥（打乱的字母表）确定了，密钥字不同，也会产生不同的密文，即非固定式对应。 加解密在之后的表述中：以<密钥>表示26字母顺序表以<密钥字>表示输入的一串辅助加密的消息序列 现假定输入的密钥字为k1到km，总长为m个字母；明文为x1到xm；表字母以初始26字母顺序表为例，进行加解密说明： 加密 维吉尼亚密码的加密定义如下：即： 将明文分成若干个分组，每个分组为m个字母长度（即密钥字的长度）； 再找出分组中的字母和密钥字的字母在代换表中的对应数字； 将其对应位两两相加得出的数字，再代入代换表中，查出对应的密文字母； 将所有明文分组都如此操作，即得到密文。 加密示例： 字母表为原始A-Z因此00对应A，……，25对应Z； 输入密 ...

简述代换密码是古典密码中的典型例子，采用单表代换的方式进行加密。 单表代换即在原始顺序的26个字母表的基础上，通过改变字母位置而生成无序的26字母表，该字母表就是本次加密的密钥。 比如在下表中，大写字母即初始字母表，其对应的小写字母，就是变换顺序后的字母表，也就是密钥。因为代换密码的密钥是26个字母的排列组合，因此该加密算法的密钥空间为26！，与凯撒密码相比，如果对代换密码进行穷举搜索的方式进行攻击，计算量会相当大。 加解密 加密过程 作为古典密码，代换密码的加密过程很简单，当给出本次加密的密钥时，只需要将明文字母用其对应的密钥字母进行替代，就完成了加密。 比如置换表如下：当明文是“ENCRYPT”时，其对应的密文就是“tfeknhz”。 解密过程 由于代换密码的加密实质是形成明文与密文的一一映射关系，因此解密过程和加密相同，其实就是将密文对照其加密所用的置换表，得出明文。 由上述置换表得出其逆置换表：再将刚才的密文“tfeknhz”逐一查找，即得出明文“ENCRYPT”。 代码实现 思路 使用代码实现主要分一下三个步骤： 1、生成随机置换表（即：初始字母表和随机的密钥字母表） ...

简介移位加密是一种古典的替换加密技术，明文中的所有字母都在字母表上向后（或向前）按照一个固定数目进行偏移后被替换成密文。例如：当偏移量是3的时候，所有的字母A将被替换成D，B替换成E，此时的加密方式称为凯撒密码。 此程序进行动态录入移位数，称之为密钥；并且仅支持输入大小写字母。 思路： 利用取余的方式实现移位 代码实现加密过程123456789101112131415161718192021222324#include <stdio.h>#include <stdlib.h>/* 加密 */int main(){ int key = 0; char word_1[50] = "\0"; //加密前 char word_2[50] = "\0"; //加密后 int i = 0; printf("输入明文："); scanf("%s", word_1); printf("输入密钥："); scanf( ...