简述
公钥密码
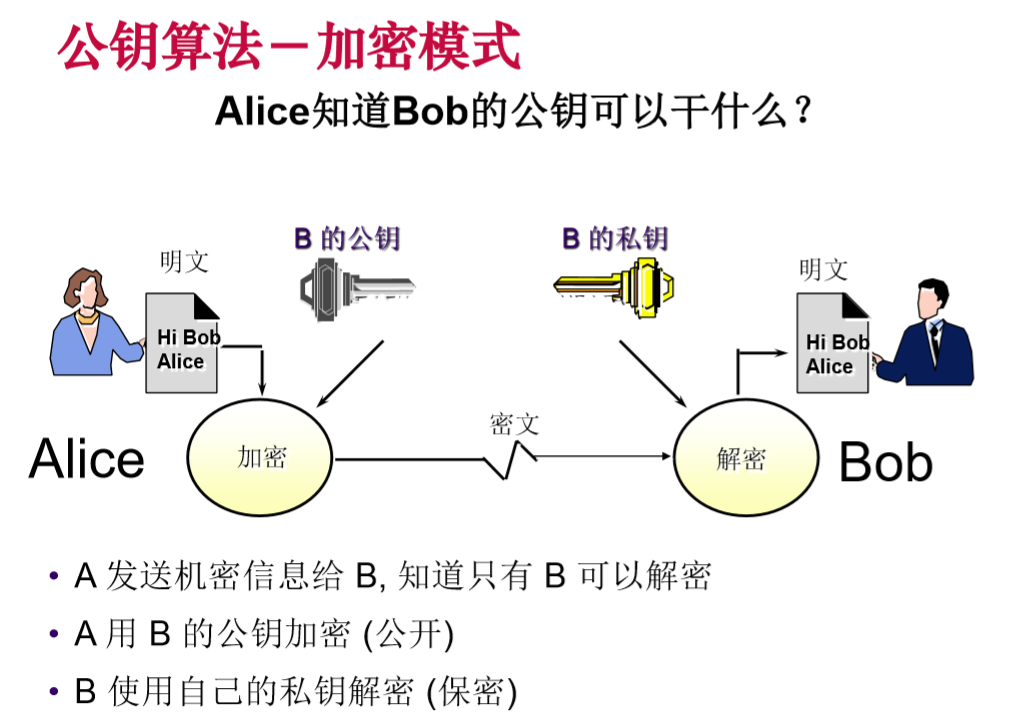
公钥密码又称非对称密码,所谓非对称密码即加解密使用的不是同一个密钥。
在公钥密码体系中,使用每个人拥有两种密钥,公钥和私钥,公钥是公开的,用来加密,私钥是私自保存的,用于解密。如:
公钥密码将辅助信息(陷门信息)作为私钥,这类密码的安全强度取决于它所依据的问题的计算复杂度。
常见的公钥密码有RSA公钥密码、ElGamal公钥密码、椭圆曲线密码。
背包问题
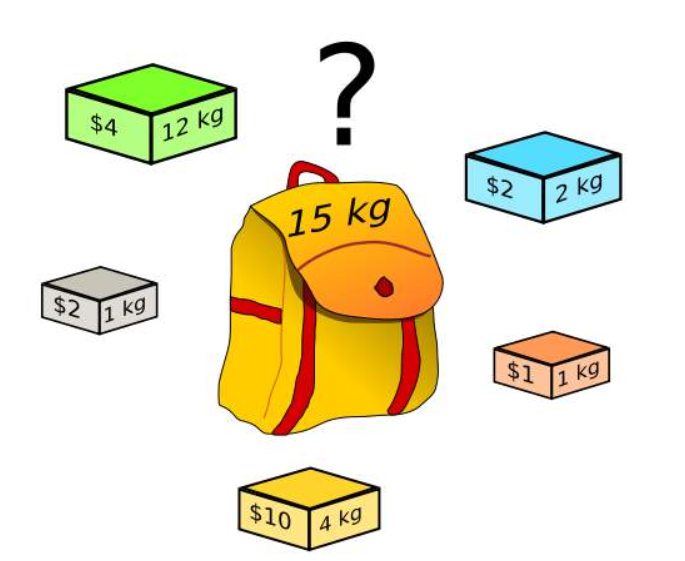
背包问题:假设有一堆物品,体积各不相同,问能否从这堆物品中找出几个正好装满一个给定容量的背包?(假定物品之间不留空隙)b1v1+b2v2+…+bnvn=C,其中,bi(i=1,2,…,n)等于1或者0。
bi = 1表示第i个物品在背包中,bi=0表示第i个物品不在背包中,称物品体积的序列(v1,V2,…,vn)为背包向量。
目前没有一个高效的算法来解决这个问题,只是进行穷举式搜索,但当数据足够多时,达到2的1024或2048位时,穷举式搜索将不再现实,问题就很复杂了。
超递增背包
并非所有的背包问题都没有有效算法,有一类特殊的背包问题是容易求解的,这就是超递增背包问题。
设V=(v1,2,…,vn)是一个背包向量,若V满足V中每一项都大于它前面所有项之和 ,则称V是一个超递增向量,或者称序列v1,V2,,n是一个超递增序列,以V为背包向量的背包问题被称做超递增背包问题。
比如,序列1,2,4,16,…… ,2^n就是一个超递增序列。
超递增背包问题的解可以通过以下方法找到:
假设背包容量为C,从右到左依次检查超递增背包向量中的每一个元素Vi,如果C >= Vi,则C = C - Vi,并将对应的bi置为1,否则跳过,继续检查下一元素,直至遍历完所有元素。如果此时C等于0,则该超递增背包问题有解,解为bi中的1对应的超递增背包向量中的元素,否则表示该问题无解。
例如:
加解密 背包算法具体如下:私有密钥设置为将一个超递增向量 V 转换为非超递增向量 U 的
加密
首先将二进制明文消息划分成长度与非超递增向量U长度相等的明文分组b1 b2 …… bn;
然后计算明文分组向量 B =(b1,b2,……,bn)与非超递增向量 U= (u1,u2,……,un)的内积 B * U = b1u1 + b2u2+ ……+bnun,所得结果为密文。
解密
先还原出超递增背包向量V = t的逆元 * U mod k=t * t的逆元 * V mod k;
再将密文 B * U 模 k 乘以 t逆元 的结果作为超递增背包问题的背包容量,求解超递增背包问题,得到消息明文。
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 import randomfrom my_modules import modulesdef init (length, interval ): listV = [] listV_b = [] bagCapacity = 1000 for i in range (length): listV.append(sum (listV) + random.randrange(1 , interval)) listV_b.append(0 ) bagCapacityTmp = bagCapacity for i in range (len (listV)-1 , -1 , -1 ): if bagCapacityTmp >= listV[i]: bagCapacityTmp -= listV[i] listV_b[i] = 1 return listV def creatPKey (listV ): while True : k = int (input ("输入私钥k(大于%d):" % (sum (listV)))) if k <= sum (listV): continue while True : t = int (input ("输入私钥t(与k互素):" )) if not modules.judgeCoPrime(k, t): continue break break inverse_t = modules.getInverse(t, k) return k, t, inverse_t def creatSKey (listV, t, k ): sKeyList = [] for i in listV: sKeyList.append(i * t % k) return sKeyList def encrypt (massage, sKeyList ): massageList = [] ciphertextList = [] while len (massage) % len (sKeyList) != 0 : massage = "0" + massage for i in range (int (len (massage) / len (sKeyList))): start = (i * len (sKeyList)) end = ((i + 1 ) * len (sKeyList)) massageList.append(massage[start : end]) for i in massageList: multiplyList = list (map (lambda x, y: int (x) * int (y), list (i), sKeyList)) ciphertextList.append(sum (multiplyList)) return ciphertextList def decrypt (massage, sKeyList, k, inverse_t ): pliantextList = [] reductListV = [] for i in sKeyList: reductListV.append(int (i) * inverse_t % k) bagCapacityList = [] for i in massage: bagCapacityList.append(int (i) * inverse_t % k) for bagCap in bagCapacityList: pliantextTmp = [] for i in range (len (reductListV)): pliantextTmp.append(0 ) for i in range (len (reductListV) - 1 , -1 , -1 ): if bagCap >= reductListV[i]: bagCap -= reductListV[i] pliantextTmp[i] = 1 pliantextList += pliantextTmp start, end = 0 , 0 for i in range (len (pliantextList)): if pliantextList[i] != 0 : break end = i + 1 del pliantextList[start : end] pliantextList = map (str , pliantextList) pliantext = "" .join(pliantextList) return pliantext if __name__ == "__main__" : length, interval = 8 , 4 listV = init(length, interval) print ("初始向量:" , listV) k, t, inverse_t = creatPKey(listV) print ("\n私钥验证成功,分别为 <k:%d>, <t:%d>,<t逆元:%d>" %(k, t, inverse_t)) sKeyList = creatSKey(listV, t, k) print ("公钥向量为:" , sKeyList, "\n" ) while True : choice = input ("1、加密 2、解密\n请选择:" ) if choice == "1" : massage = input ("输入明文(01序列):" ) ciphertextList = encrypt(massage, sKeyList) print ("加密结果:" , ciphertextList) elif choice == "2" : ciphertextList = list (map (int , list (input ("输入密文:" ).split("," )))) sKeyList = list (map (int , list (input ("输入公钥向量:" ).split("," )))) k = int (input ("输入密钥k:" )) inverse_t = int (input ("输入密钥t逆:" )) pliantext = decrypt(ciphertextList, sKeyList, k, inverse_t) print ("解密结果:" , pliantext)
其中,from my_modules import modules 为导入我自己的一个模块,因为使用频率高,内容为在写密码学代码中常用的判断互质和求逆元。moduls文件内容如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 def judgeCoPrime (a, b ): def maxCommonFactor (m, n ): result = 0 while m % n > 0 : result = m % n m = n n = result return result if maxCommonFactor(a, b) == 1 : return True return False def getInverse (a, b ): def extGcd (a_, b_, arr ): if b_ == 0 : arr[0 ] = 1 arr[1 ] = 0 return a_ g = extGcd(b_, a_ % b_, arr) t = arr[0 ] arr[0 ] = arr[1 ] arr[1 ] = t - int (a_ / b_) * arr[1 ] return g arr = [0 ,1 ,] gcd = extGcd(a, b, arr) if gcd == 1 : return (arr[0 ] % b + b) % b else : return -1
代码细节
总述
整体思路分为5个步骤,分别是初始化超递增向量、创建私钥、利用初始化和私钥产生公钥、利用公钥对明文加密、利用公钥私钥和密文进行解密。
其中较复杂的是在加密和解密两个环节。
由于python中的众多列表、字符串方法,如map、lambda、join,以及类似于通过list[a:b]来访问list的[a, b)下标元素,得以让程序看起来简洁。如若是C语言,则代码量看起来会稍多一些。
massageList.append(massage[start : end])
出现在加密部分中的明文分组操作中,massage为输入的明文字符串。
作用是将明文massage中的start号元素到end号元素作为一个整体,添加到明文分组列表massageList中;目的是根据超递增背包向量的长度,来对明文进行分组。
该访问方法可访问字符串和列表。
del pliantextList[start : end]
出现在解密部分中的去除扩充的0操作中,pliantextList为解密出来的明文列表。
作用:删除pliantextList中下标在区间[start, end)内的元素
for i in range(len(listV)-1, -1, -1)
出现在求超递增背包解的步骤中,listV为超递增向量。
作用:从后往前访问列表元素(以下标形式)。
除此,逆向访问列表元素的方法还有list[::-1]:
1 2 3 list1 = [1 , 2 , 3 , 4 , 5 ] print (list1[::-1 ])
k, t, inverse_t = creatPKey(listV)
出现在调用创建私钥函数,接收返回值部分。
creatPKey()函数的返回值为:return k, t, inverse_t,接收时只需要连续写相应个数的变量来接收即可。
这是与C语言等其他语言不同的地方:python函数可以有多个返回值 。
list(map(lambda x, y: int(x) * int(y), list(i), sKeyList))
出现在加密部分的内积操作中,其中list(i) 和 sKeyList皆为列表。
作用:通过map()将两个列表的对应位元素逐个应用在lambda定义的函数上,该函数作用是“传入两个参数,返回这两个数整形类型的乘积”,再将所有结果组成的数据块转换为列表格式。
加密测试
输入length(向量元素个数)和interval(随机增量最大值)
输入 length:8
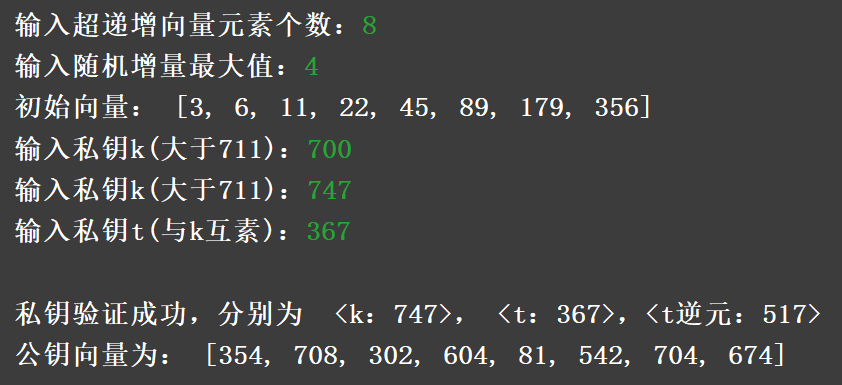
产生一个随机的超递增向量:[3, 6, 11, 22, 45, 89, 179, 356]
输入 k(大于向量的所有元素和) 和 t(与k互质)
输入 k:747
此时私钥和公钥都产生:
私钥 : <k:747>, <t:367>,<t逆元:517>
公钥 : [354, 708, 302, 604, 81, 542, 704, 674]
加密
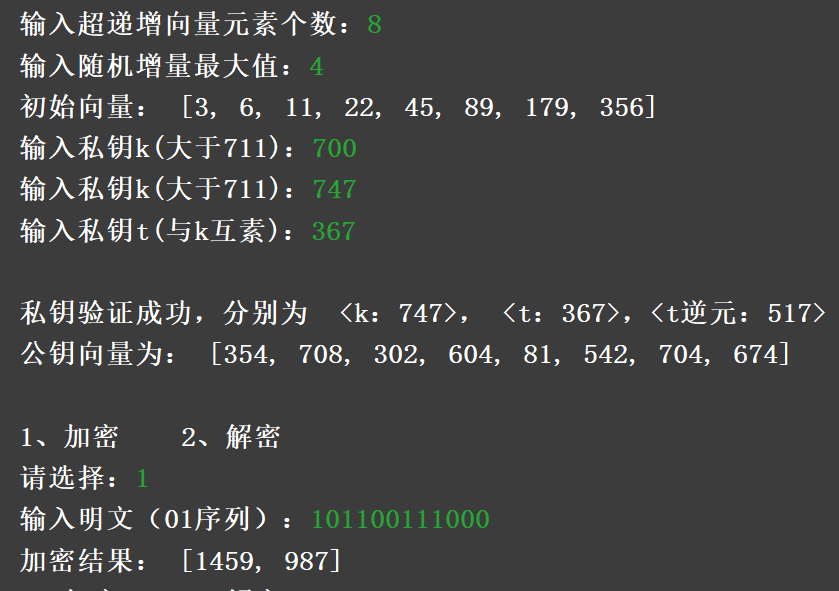
输入明文:101100111000
加密结果:1459, 987
因为位数大于向量长度,因此进行了分组,产生了两个密文数字。
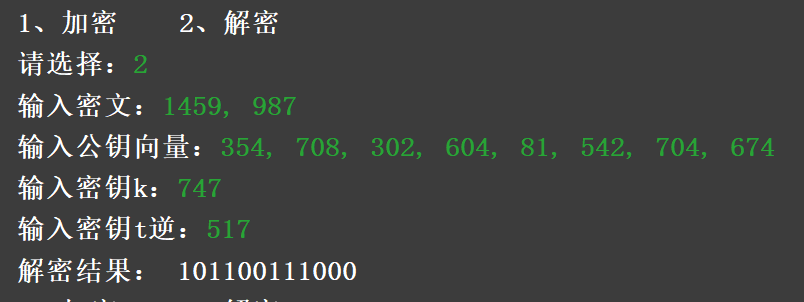
解密
输入密文:1459, 987
解密结果: 101100111000