简述

RSA加密算法是一种非对称加密算法。在公开密钥加密和电子商业中RSA被广泛使用。

整个加密过程要用到p、q、n、L、E、D六个数据：

p、q：选取两个足够大的素数 p、q
n：令 n = p * q
Fn：Fn 是 n 的欧拉函数，（此处为（p-1）乘以（q-1））
e：选取一个e使得 1 < e < Fn，且 gcd(e，Fn) = 1
d：d 为 1 = e mod Fn 的乘法逆

此时，
（e，n）为公钥
（d，n）为私钥

加密过程：c = ( m ^ e ) % n

解密过程：m = ( c ^ d ) % n

代码实现

# 判断素数
def judgePrimeNumber(num):
    # 不能被2~sqrt(m)（取整）之间的整数整除的数即素数
    sqrtResult = int(num **0.5)
    for i in range(2, sqrtResult + 1):
        if num % i  == 0:
            return False
    return True

# 判断互质
def judgeCoPrime(a, b):
    # 求最大公因数
    def maxCommonFactor(m, n):
        result = 0
        while  m % n > 0:
            result = m % n
            m = n
            n = result
        return result
    if maxCommonFactor(a, b) == 1:
        return True
    return False

# 求逆元
def getInverse(a, b):
    # 扩展的欧几里得
    def extGcd(a_, b_, arr):
        if b_ == 0:
            arr[0] = 1
            arr[1] = 0
            return a_
        g = extGcd(b_, a_ % b_, arr)
        t = arr[0]
        arr[0] = arr[1]
        arr[1] = t - int(a_ / b_) * arr[1]
        return g
    # 求a模b的乘法逆x
    arr = [0,1,]
    gcd = extGcd(a, b, arr)
    if gcd == 1:
        return (arr[0] % b + b) % b
    else:
        return -1

# 产生密钥（n，e为公钥，d为私钥）
def cerateKey(p, q):
    n = p * q
    n_Euler = (p - 1) * (q - 1)
    while True:
        e = int(input("选择公钥e（1 < e < %d 且e与%d互质）：" %(n_Euler, n_Euler)))
        if 1 < e < n_Euler and judgeCoPrime(e, n_Euler):
            break
    d = getInverse(e, n_Euler)
    return n, e, d

# 加密
def encrypt(n, e, plaintext):
    plaintextList = []  # 分组后的明文列表
    ciphertextList = [] # 密文列表
    i = 0
    # 按n的位数减位判断
    while i < len(plaintext):
        j = len(str(n))
        while True:
            if int(plaintext[i:(i + j)]) < n:
                plaintextList.append(int(plaintext[i:(i + j)]))
                i += j
                break
            j -= 1
    # 加密
    for item in plaintextList:
        cipherText = item ** e % n
        ciphertextList.append(cipherText)
    return ciphertextList

# 解密
def decrypt(d, n, ciphertextList):
    plaintext = ""
    plaintextList = []
    for item in ciphertextList:
        plaintext += str((item ** d % n))
    return plaintext

# 输入数据
def inputData():
    while True:
        p = int(input("输入p（素数）："))
        if judgePrimeNumber(p):
            break
    while True:
        q = int(input("输入q（素数）："))
        if judgePrimeNumber(q):
            break
    return p, q

if __name__ == "__main__":
    while True:
        print("—————RSA算法—————")
        choice = input("1、加密        2、解密\n请选择：")
        if choice == "1":
            p, q = inputData()
            n, e, d = cerateKey(p, q)
            print("————————————————————")
            print("| 公钥n：%d | 公钥e：%d | 私钥d：%d |" % (n, e, d))
            print("————————————————————")
            massage = input("输入明文：")
            ciphertextList = encrypt(n, e, massage)
            print("加密结果：", ciphertextList)
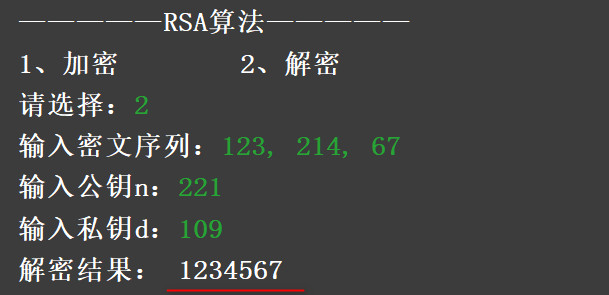
        elif choice == "2":
            ciphertextList = list(map(int, list(input("输入密文序列：").split(","))))
            n = int(input("输入公钥n："))
            d = int(input("输入私钥d："))
            plaintext = decrypt(d, n, ciphertextList)
            print("解密结果：", plaintext)